
乱数が日常生活で幅広く使われていることを本書は教えてくれる ――世論調査とか、くじ引きとか。
製品宣伝キャンペーンの応募番号も。ゲームとも深い関係にある。初期値しだいで、シナリオが変わりますね。
疑似乱数の研究で日本人の研究が大きく寄与しているとは興味深い。
でたらめな数字の並びのことを「乱数」と呼んでいる。理想的なサイコロのように、どの目が出る確率も同じで、次に何が起きるのかを予測できない現象からつくられる数字の並びだ。
より正確には、「コルモゴロフ・チャイティンによる定義」というのがある、「その数字を並べる以上に短くその数列を記述できる方法がない」。
何らかの規則性があれば、その数列は圧縮可能であり短く記述できる。乱数はルールや特徴がなく、圧縮できない。
つまり、覚えるには丸暗記しか方法がないのだ。その数字の並びを説明しようとしたら、それ自身を見せるしかない。
乱数の用途は幅広い。まずは無作為抽出(ランダムサンプリング)に使われること。くじ引きとか、抜取検査や薬の効果を調べる試験、世論調査などで利用されている。
コンピューターによる数値計算でも使われている。シミュレーション――直接観察できない現象をコンピューターの中で再現して性質を調べること。
暗号など情報セキュリティーの分野でも乱数は重要な役割だ。
乱数の少ない「乱数表」で世論調査の対象者を選んでいると、繰り返し使っているうちに同じ人を選んでしまう危険性がある。
工業製品の抜取検査でも、同様の問題が起る。そうすると世論調査の結果や、製品の不良率推定に偏りが出てしまう。乱数には偏りがなく、真にランダムであること ――質の良さが求められる。
π(パイ)はなかなかよい乱数であるという。研究者によれば、200万桁のπ(パイ)について、乱数としての善し悪しを調べると、0〜9の数字の出現頻度や、
次に来る数字に癖がないかどうかなど、伝統的なテストをいずれもパスしたという。「200万桁のπ(パイ)は、計算機の性能の証拠というだけでなく、乱数の標準ともなる」との情報処理学会の発表もあった。
乱数には大きく分けて、物理乱数と疑似乱数の2つがある。物理乱数はサイコロのように、もともとランダムな自然現象を利用するもの。
高度なものでは、放射性物質の崩壊や電気回路に発生するランダムなノイズを使うものがある。特に質の高い乱数が求められる情報セキュリティー分野などで使われる。
物理乱数は再現性がないのが特徴だ。
疑似乱数はプログラムでつくられる。数値計算や世論調査、コンピューターゲームなどで使われる。最近の数値計算では,何億個、何兆個という乱数が使われ、疑似乱数の需要が広がっている。
疑似乱数の最先端、「メルセンヌ・ツイスター(MT)」は日本で開発されたそうだ。考案者は松本眞・西村拓士の両氏。
線形合同法の欠点を克服し繰り返しの周期が極めて長いことが保証されたという(2の19937乗マイナス1)。
このMTアルゴリズムは、JISやISOにも採用され、各種のソフト――C言語とかExcel(RAND関数)にも組み込まれている。
情報セキュリティ分野でも乱数が大きく関わっている。20世紀に入ると特殊な暗号器を使う軍事用途の複雑な暗号が開発された。
第2次世界大戦時にドイツ軍が使っていた「エニグマ」が代表的。1970年代以降、情報をインターネットで流通させるときに使われる暗号は、さらに重要性を増した。
暗号鍵を毎回変える際に乱数を使っている。素因数分解により、公開鍵から秘密鍵を推測するためには、膨大な計算時間がかかる設計なので安全である。
コンピューターの進歩とともに、「乱数を使う数値計算」の世界が急速に拡大してきた。数値計算法の代表がモンテカルロ法。太陽内部の核融合反応を人工的に起こす発電の研究でも基本は同じ。
防災にも応用されている。地震が起きたとき都市の建物がどのように揺れるのかの大規模なシミュレーション。
揺れの計算の前提となる内部構造に乱数でばらつきを取り入れて何度も計算を繰り返して揺れを推定する。モンテカルロ法による計算1回は、大きな地震が1回起きたことに相当する。
…………………………………………………………………………………………………………
【モンテカルロ法とは】πを計算で求める手順
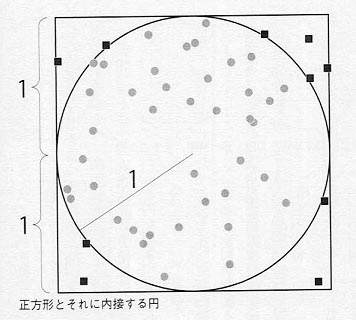
「半径1の円」を、ちょうど取り囲むように「1辺2の正方形」を描く
・上から豆を落とす。そして、豆が円の内側に落ちた回数を数える
・その回数を、豆を落とした回数で割ると、円の内側に豆が入る確率を計算できる
・豆を落とす回数を増やしていけばその確率が、円の面積/正方形の面積 に近づく
・確率が70%(0.7)であれば、正方形の面積は2×2=4とわかっているので
円の面積=4×0.7=2.8 ⇒ πの近似値として2.8を得る。
*豆の落とし方に偏りがあるとπを精度よく見積もることはできない
…………………………………………………………………………………………………………
◆ 『でたらめの科学 サイコロから量子コンピューターまで』 勝田敏彦、朝日新書、2020/12